数据结构03-跳跃表
数据结构03-跳跃表
总览
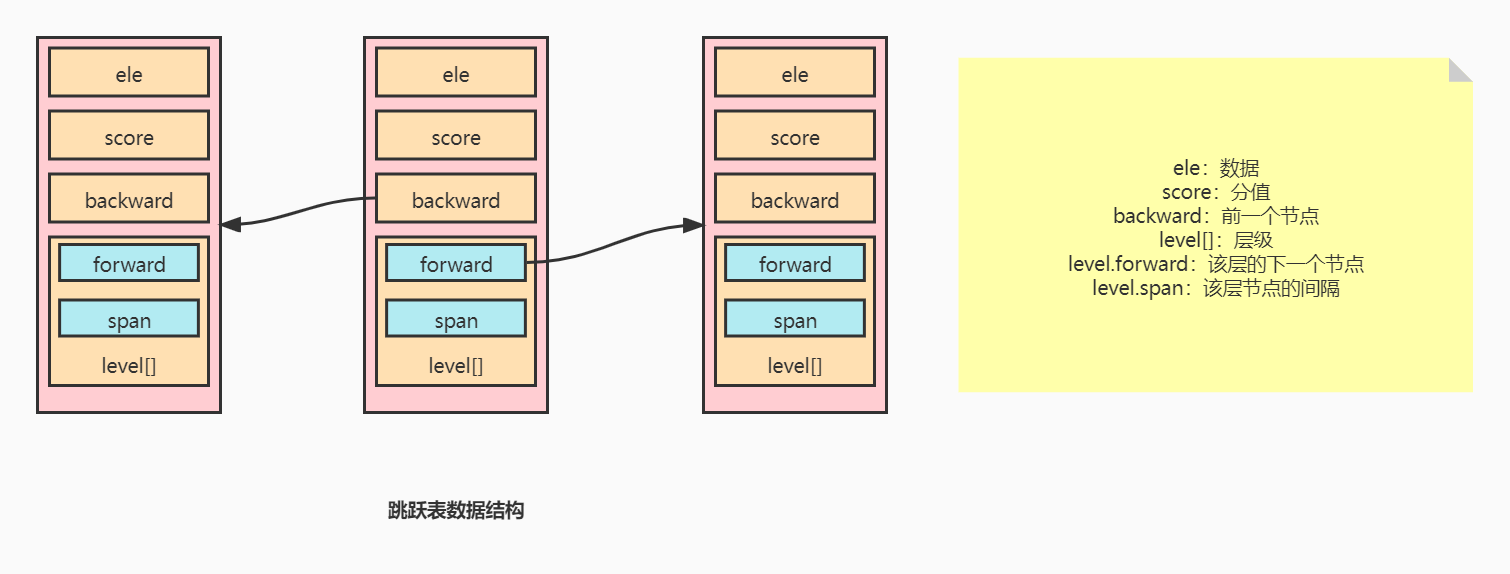
分析
跳表是一个非常优秀的数据结构,优秀在性能媲美红黑树,优秀在实现起来比红黑树简单(跳表实现也不是很简单)。在一个有序的数组中,我们可以使用二分查找来定位节点的位置,但在普通的链表中则不能,需要把链表从头到尾遍历一个,时间复杂度是O(n)。实际上,我们在链表的基础上做一点改造就能实现类似二分查找的数据结构,这就是链表。
普通的链表数据结构如下:

跳跃表就是把单链表改成了多链表组合而成的数据结构,如下:

这么一来,在链表中查找节点的性能就提高了,怎么体现呢?以上面的图为例子,我需要查找node5节点
在普通的链表中,链路是这样的:
node1 -> node2 -> node3 -> node4 -> node5,经过4个节点。
在跳表中,链路是这样的:
node1 -> node3 -> node4 -> node5,经过3个节点。
可以看出跳表通过不同层级的表之间的跳跃,实现节点间不连续,从而加速了链表的查找性能,在上面的例子中可能体现不是很明显,但在数据量大的情况下,效果会非常明显,能达到类似二分查找的效果。
redis实现
如果能理解上面的原理,实现一个跳表不难了,从单链表向多链表改写,处理节点间的关系
数据结构
typedef struct zskiplistNode {
/* 节点数据 */
sds ele;
/* 分值 */
double score;
/* 上一个节点 */
struct zskiplistNode *backward;
struct zskiplistLevel {
struct zskiplistNode *forward;
/* 距离下一个节点的间隔,遍历下去可以知道某个节点在什么位置 */
unsigned long span;
} level[];
} zskiplistNode;
typedef struct zskiplist {
/* 首尾节点 */
struct zskiplistNode *header, *tail;
/* 链表长度 */
unsigned long length;
/* 等级 */
int level;
} zskiplist;
随机层级
在插入一个节点的时候,会通过一个随机函数来决定该节点的层级,如是2层,这节点就会在两个层级中出现,先上图的node4节点。
随机层级的算法
int zslRandomLevel(void) {
int level = 1;
/* ZSKIPLIST_P是0.25
ZSKIPLIST_MAXLEVEL是32,层级最大是32层
*/
while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
level += 1;
return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}
while中的条件random()&&0xFFFF产生一个0xFFFF范围内的数字,判断是否小于0.25 * 0xFFFF,如果小于level+1。这里就是随机造层的核心算法
"幂次法则"也叫“80-20法则”,由经济学家维尔弗雷多.帕累托在1906年提出,他认为:在任何一组东西中,最重要的只占其中一小部分,约20%,其余80%尽管是多数,却是次要的。--百度百科
利用幂次法则(二八定理)来产生level,层级越高几率越小。
插入逻辑
/* Insert a new node in the skiplist. Assumes the element does not already
* exist (up to the caller to enforce that). The skiplist takes ownership
* of the passed SDS string 'ele'.
* 步骤:
* 1、找出每个层级插入的位置
* 2、根据次幂法则随机生成新插入的节点的层级
* 3、遍历生成的层级在对应位置插入节点
* 4、更新节点的间隔
* 5、赋值新增节点的上一个节点(backward)
* 6、更新链表长度
* */
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
/* update的作用是记录在每一层插入的位置 */
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
unsigned int rank[ZSKIPLIST_MAXLEVEL];
int i, level;
serverAssert(!isnan(score));
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
/* store rank that is crossed to reach the insert position */
rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
/* 当前节点的分数小于新增的分数 或者 (当前节点的分数等于新增的分数 并且 当前节点数据小于新增节点数据)
* 这个while循环的作用是记录间隔 和 找出插入新节点的位置
* */
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
/* 记录层级的间隔 */
rank[i] += x->level[i].span;
/* 指向下一个节点继续上面的逻辑 */
x = x->level[i].forward;
}
/* 最靠近需要插入节点的分数的节点 */
update[i] = x;
}
/* we assume the element is not already inside, since we allow duplicated
* scores, reinserting the same element should never happen since the
* caller of zslInsert() should test in the hash table if the element is
* already inside or not. */
/* 次幂法则(二八法则)level越大出现的机率越小 */
level = zslRandomLevel();
/* 随机生成的层级大于原来的层级 */
if (level > zsl->level) {
/* 把新的层级节点都指向头部 */
for (i = zsl->level; i < level; i++) {
rank[i] = 0;
update[i] = zsl->header;
/* 间隔是链表的长度,因为是新的一层,间隔就是链表的长度 */
update[i]->level[i].span = zsl->length;
}
zsl->level = level;
}
/* x是新建的节点 */
x = zslCreateNode(level,score,ele);
/*
* 新增节点:x
* 原来有的节点:o
*
* o - o 循环后在两个o之间插入x,变成
* o - x - o
* */
for (i = 0; i < level; i++) {
/* 这一步相当于把原来节点的下一个节点 分配给 新的节点的下一个节点 */
x->level[i].forward = update[i]->level[i].forward;
/* 原来节点的下一个节点 指向 新建节点 */
update[i]->level[i].forward = x;
/* == 这里注意一下,新增节点的上一个还没有赋值 == */
/* update span covered by update[i] as x is inserted here */
/* 更新span */
x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}
/* increment span for untouched levels 把level以上的层级span+1,因为上面的循环没有更新到level以上的层级 */
for (i = level; i < zsl->level; i++) {
update[i]->level[i].span++;
}
/*
* ==在这里给新增节点的上一个赋值==
* 给新的节点关联上一个节点,为什么是update[0]?因为第1层的间隔是1,update[0]就是这个
* 新增节点的上一个
* */
x->backward = (update[0] == zsl->header) ? NULL : update[0];
/* 如果第1层的下一个节点不为空(在链表的节点间插入值,比如在10与12之间插入11) */
if (x->level[0].forward)
/* 更新节点的上一个节点 */
x->level[0].forward->backward = x;
else /* 为空的话说明是在尾部插入,把链表的tail指向新的节点 */
zsl->tail = x;
/* 长度+1 */
zsl->length++;
return x;
}
查找逻辑
zskiplistNode *zslFirstInRange(zskiplist *zsl, zrangespec *range) {
zskiplistNode *x;
int i;
/* If everything is out of range, return early. */
if (!zslIsInRange(zsl,range)) return NULL;
x = zsl->header;
/* 大概的意思就是从跳表的最高层级开始遍历,在同一层级中不断取下一个节点的
* 分数来判断是否小于区间的最小值,如果成立,继续遍历这个节点的下一个层级
* 重复上面的逻辑,直到把所有层级遍历完
*
* 作用:从大往小缩进,取到在区间范围内的最小值
* */
for (i = zsl->level-1; i >= 0; i--) {
/* Go forward while *OUT* of range. */
while (x->level[i].forward &&
!zslValueGteMin(x->level[i].forward->score,range))
x = x->level[i].forward;
}
/* This is an inner range, so the next node cannot be NULL. */
x = x->level[0].forward;
serverAssert(x != NULL);
/* Check if score <= max. */
/* 判断分数是否大于最大值 */
if (!zslValueLteMax(x->score,range)) return NULL;
return x;
}
删除逻辑
int zslDelete(zskiplist *zsl, double score, sds ele, zskiplistNode **node) {
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
int i;
x = zsl->header;
/* 从高到低遍历每个层级 */
for (i = zsl->level-1; i >= 0; i--) {
/*
* 满足一下条件,指针向前移动:
* 1、层级的下一个节点(x)不为空
* 2、x的分值小于传进来的分值,或者分值相等的情况下,x的数据
* 字节长度小于传进来的数据的字节长度
* */
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
x = x->level[i].forward;
}
update[i] = x;
}
/* We may have multiple elements with the same score, what we need
* is to find the element with both the right score and object. */
x = x->level[0].forward;
/* 因为在一个链表中可能有有多个分值相同的节点,在分值相同的情况下,还需要对比数据 */
if (x && score == x->score && sdscmp(x->ele,ele) == 0) {
/* 删除节点 */
zslDeleteNode(zsl, x, update);
if (!node)
/* 回收内存 */
zslFreeNode(x);
else
*node = x;
return 1;
}
return 0; /* not found */
}
总结
跳表相对于普通的链表来说,性能是提高了,但是占用的内存更多。使用空间换时间的设计思路,通过构建多级索引来提升查询性能,支持快速地插入、删除、查找操作,时间复杂度都是O(logn)。在JAVA中没有默认的跳表实现,可以动手实现一下。
